Have you ever wondered why there are exactly 12 musical notes? It is said to have been discovered by Pythagoras, but with some knowledge of mathematics and basic physics, one might be able to discover it on their own. Here, I will gradually explain with hints along the way, so please consider and ponder. Once you exclaim, “Ah, 12 is indeed the best!” you will achieve complete understanding.
Start Question
First, as a basic premise, musical pitch is determined by the frequency of sound waves. Notes whose frequencies form simple integer ratios harmonize well with each other. From here, we begin with the following two principles:
- When the frequency ratio is 1:2, the harmony is extremely strong.
- When the frequency ratio is 1:3, the harmony is quite strong.
Perhaps this is because the human eardrum has a structure similar to string vibrations. Please proceed without doubting this aspect.
These two principles alone lead to the derivation of the 12-tone scale. If you understand just this much, you might consider yourself as having an IQ akin to Pythagoras.
Hint 1
Let’s start with the first hint: If we apply the above theorem to the current 12-tone scale of music, we get the following characteristics.
- When the frequency is doubled, the pitch goes up an octave.
- When the frequency is tripled, it goes up an octave and five degrees.
I describe them in the following figure.
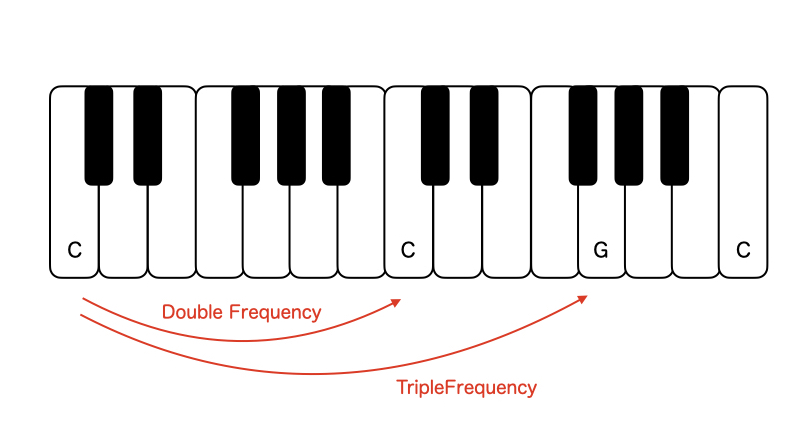
Doubling the frequency of the note C results in the higher octave C. Furthermore, tripling the frequency of the note C leads to G, which is not only an octave higher but also a perfect fifth above the octave. It’s understandable that C and C harmonize well together. G, being the dominant note relative to C, harmonizes next best after C. Please think about how these hints alone can lead to the derivation of the 12-tone scale.
Hint 2
Let’s focus on the note G (fifth) with a frequency triple that of the base note. Since doubling the frequency raises the pitch by an octave, halving the frequency lowers it by an octave. Therefore, halving the frequency of the note G, which is triple the base frequency, results in the G note an octave lower. In relation to the reference note C, the frequency of this lower G note is 1.5 times the frequency of the base note C (triple times halved). This means each 1.5-fold increase in frequency ascends by a perfect fifth. Let’s illustrate this with a diagram.
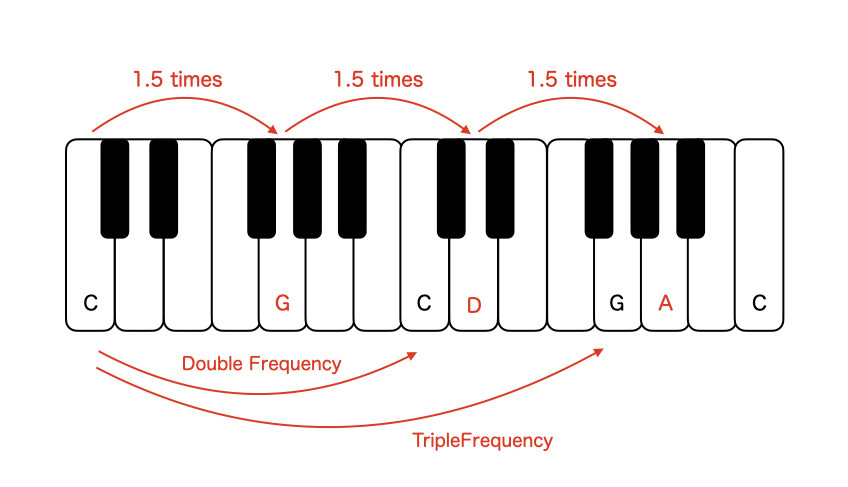
If you multiply the frequency of the note G by another 1.5, you get the note D, which is a perfect fifth above G. Further multiplying the frequency of D by 1.5 leads to the note A, which is a perfect fifth above D. (If the concept of a perfect fifth is unclear, consider it as approximately seven semitones.)
With this hint, let’s consider how we can derive the 12-tone scale. For those who noticed a resemblance to the dominant motion, you’re almost at the goal.
Hint 3
From the clue above, let’s think about what happens if we keep multiplying by 1.5. First, if we multiply by 1.5 twice, we get 2.25 times. Now, let’s write the value of the power of 1.5 in the table below. Round off the third decimal place, and write it in two decimal places.
| Power of 1.5 | Value |
| 1 | 1.5 |
| 2 | 2.25 |
| 3 | 3.38 |
| 4 | 5.06 |
| 5 | 7.59 |
| 6 | 11.39 |
| 7 | 17.09 |
| 8 | 25.63 |
| 9 | 38.44 |
| 10 | 57.67 |
| 11 | 86.50 |
| 12 | 129.75 |
| 13 | 194.62 |
| 14 | 291.93 |
I’ve written 1.5 to the power of 12 in bold. Does something click? Here’s a hint: ‘Humans don’t notice slight frequency differences.’ Let’s think about nearby integers.
Hint 4
With the previous hint, we found that 1.5 to the power of 12 equals approximately 129.75. For comparison, if it were exactly 128, which is 2 to the power of 7, multiplying by 1.5 twelve times would result in a pitch that is exactly seven octaves higher, returning to the same pitch but in a higher register.
However, 129.75 is only about 1.01 times 128, meaning it’s just a 1% difference. Given the human ear’s ability to perceive slight variations in pitch, this small difference is practically indistinguishable. Therefore, in practical terms, both numbers essentially represent the same interval when it comes to musical perception. This understanding underpins the rationale for using a 12-tone equal temperament system in music, where each semitone is evenly spaced to ensure consistent harmony across different keys and instruments.
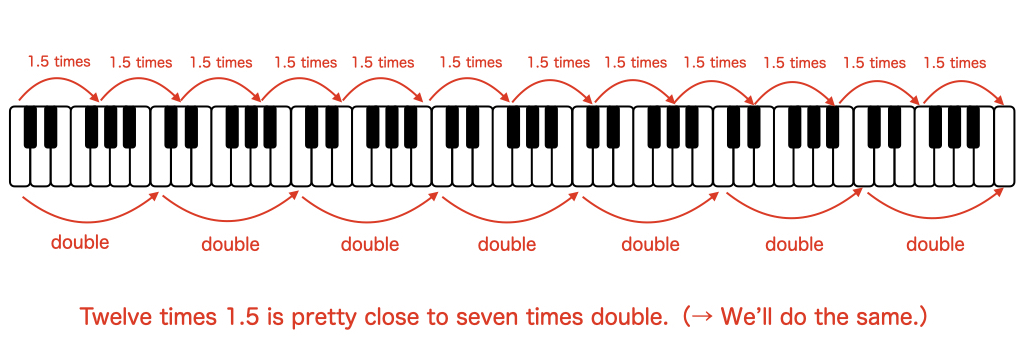
From this diagram, do you somewhat understand that there are 12 different scales? We’re almost at the finish line.
Explanation
When you raise the pitch by 1.5 times each step, you return to the same pitch after twelve increments. This means that including the initial reference pitch, you pass through twelve different pitches to return to the original pitch. If you divide the frequencies of these intermediate pitches by half, quarter, and so on, you can return to the pitches within the initial octave, creating twelve distinct pitches. Therefore, Pythagoras proposed dividing the pitches within an octave into twelve equal parts. However, there is a 1% error, which equal temperament in current music addresses by distributing this error equally among the twelve pitches.
In equal temperament, commonly used tones like C, E, and G are perfectly tuned, while the discrepancies are adjusted for other tones. This contrasts with just intonation, where all tones are perfectly tuned according to their harmonic relationships. However, in just intonation, when changing keys, the commonly used tones also change, making equal temperament more practical and widely used.
Using equal temperament, the frequencies between adjacent tones are divided equally to divide the octave’s tones into twelve equal parts, corresponding to the 12th root of 2. Let me illustrate this in a diagram.
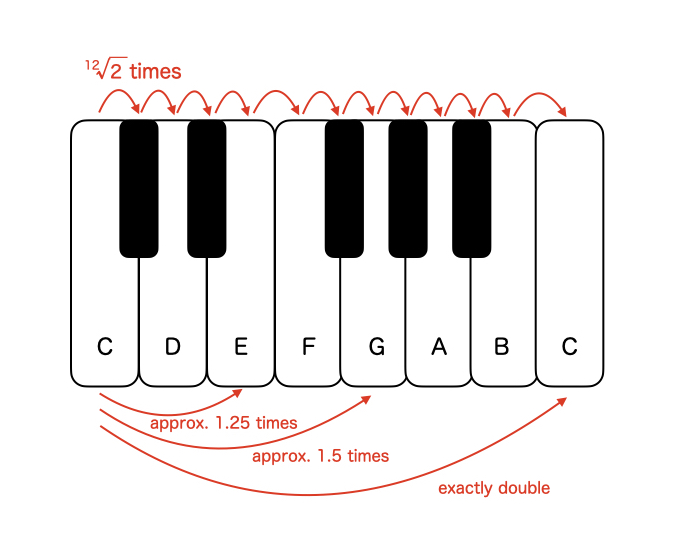
In this manner, the perfect fifth G is approximately 1.5 times the frequency, and the major third E is approximately 1.25 times. The constituent tones of a C major chord are C, E, and G. The frequency ratio of these constituent tones is 4:5:6, forming a beautiful integer ratio. This ratio constitutes the frequency relationship of a major chord and is the reason why it harmonizes pleasantly.
I will also write in the table the values that were multiplied by the twelfth power root of 2.
| Power of the 12th power root of 2 | Multiple Value | Sound Intervals (with respect to C) |
| 1 | 1.0594 | Minor 2nd |
| 2 | 1.1224 | Major 2nd |
| 3 | 1.1892 | Minor 3rd |
| 4 | 1.2599 | Major 3rd(E)approx. 1.25 times |
| 5 | 1.3348 | Perfect 4th(F)approx. 4/3 times |
| 6 | 1.4142 | Diminished 5th |
| 7 | 1.4983 | Perfect 5th(G)approx. 1.5 times |
| 8 | 1.5874 | Minor 6th |
| 9 | 1.6817 | Major 6th |
| 10 | 1.7817 | Minor 7th |
| 11 | 1.8877 | Major 7th |
| 12 | 2.0000 | Perfect 8th(C)2 times |
The notes in red are those that are particularly harmonic to the base note. If the base note is C, then E is approximately 1.25 times the base note, and G is approximately 1.5 times the base note, resulting in a C chord (composed of C, E and G) with a frequency ratio of 4:5:6. If we lower the octave of the component note of this chord, so, and consider the component note G-C-E, we also get a beautiful frequency ratio of 3:4:5, since so becomes 6->3.
3, 4, and 5 are numbers frequently seen in the Pythagorean theorem, which pertains to the conditions of a right-angled triangle. This 12-tone scale was also created by Pythagoras. Is it a coincidence, or is there some connection?
The above is an explanation of why the 12-tone scale is used. The story was a mixture of physics, mathematics and music. Once again, I think music is beautiful!